第一章 基础数学思维与技巧
最大公约数
求最大公约数----欧几里得辗转相除法
public static int gcd(int a,int b){
while(b>0){
int temp = a%b;
a=b;
b=temp;
}
return a;
}
public static int gcd(int a,int b){
return b==0?a:gcd(b,a%b);
}
最小公倍数
求最大公倍数
public static int lcm(int a,int b){
return a * b / gcd(a,b);
}
进制转换
String s = Integer.toString(a,m);//10进制a数转m进制数,结果为字符串
int a = Integer.parseInt(s,m);//把字符串s当做m进制数,将结果转为10进制数
BigInteger biginteger = new BigInteger(s,m);//把m进制的字符串s转换成10进制数后封装成大数对象
位运算
与 & (全1为1,有0为0)
判断奇偶数
奇数-二进制最后一位一定为1 偶数-二进制最后一位一定为0
public static boolean check(int m){
return (m&1)==1;
}
判断m是否为2的x次方
若m为2的x次方:m的二进制只有最高位为1,其余全为0,(m-1)的二进制除最高位都为1.
public static boolean check(int m){
return m&(m-1)==0;
}
异或 ^ (相同为0,不同为1)
找到数组中只出现了一次的数
按位异或:相同为0,不同为1
x^x=0;
0^x=x;
a^b^c=a^c^b;
public static int num(int[] s){
int ans = 0;
for(int i=0;i<s.length;i++){
ans = ans ^ s[i];
}
return ans;
}
移位 >> 和<<
8>>1 == 4
4>>1 == 2
2<<1 == 4
4<<1 == 8
n >> m == n / (2 ^ m)
n << m == n * (2 ^ m)
素数
判断素数
素数:只有1和它本身是因数 。
首先,0和1不是素数,然后 i 从 2 开始判断 i 是不是 n 的因数,如果是因数,则直接返回 n 不是素数,否则,判断 i+1是不是 n 的因数,直到 i=√n 的时候,如果 i 仍然不是 n 的因数,那么 n 就是素数。
注:如果一个数 a 能够整除 i ,那么 i 和 a/i 一定满足:假设 i<=a/i , 那么 i<=√n , && a/i>= √n 。
public static boolean isprime(int n){
if(n==0 || n==1)
return false;
for(int i=2;i<=n/i;i++){
if(n%i==0)
return false;
}
return true;
}
求1~n中的所有素数----埃氏筛法
思路:如果一个数不是素数,那么这个数一定是 n 个素数的乘积(0和1除外),同理,素数的 k 倍数一定是合数(k>=2)。
public static void isprime(int n){
boolean[] isprime = new boolean[n+1];//false表示素数,true表示合数
for(int i=2;i*i<=n;i++)
if(!isprime[i]) //i是质数
for(int j=2;j*i<=n;j++)//将i的倍数全部标记为合数
isprime[i*j] = true;
for(int i=2;i<=n;i++)
if(!isprime[i])
System.out.println(i);
}
求1~n中的所有素数----欧拉筛法
思路:每个合数,只被他最小的质因子筛一次。
注:与埃氏筛法不同,埃氏筛法是将素数的倍数,标记为合数;欧拉筛法是将目前已经找到的每一个素数的 i 倍标记为合数,无论 i 是否是素数,同时,如果 i 本身就是素数的倍数,那么就去执行下一个 i 。
public static void isprime(int n){
boolean[] isprime = new boolean[n+1];
int[] prime = new int[n];//存储素数
int count = 0;//统计目前素数个数
for(int i=2;i<=n;i++) {
if(!isprime[i]) //i是质数
prime[count++] = i;//把当前素数存储到数组中count位置
for(int j=0;j<count && i*prime[j]<=n;j++){//将i的倍数全部标记为合数
isprime[i*prime[j]] = true;
if(i%prime[j]==0) break;//欧拉筛法精髓
}
}
for(int i=0;i<count;i++)
System.out.println(prime[i]);
}
例题:最小质因子之和
题目链接:最小质因子之和(Easy Version) - 蓝桥云课 (lanqiao.cn)

思路:因为题目输入为T组数据,如果单独计算每组数据,则会有部分区间的数据被重复计算,所以先通过埃氏筛法,求出每一个数的最小质因子,将结果存放在 ans 数组中,然后将 ans 数组表示为前缀和数组,此时 ans 数组中的结果就为2~n的质因子之和,此时,题目若输入 15 ,则直接输出 ans[15] 即可。
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
public class 最小质因子之和 {
static boolean[] isprime = new boolean[3000001];//是否是素数
static long[] ans = new long[3000001];//存储最小质因子 i的最小质因子为ans[i],例:ans[4] = 2
static BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
public static void main(String[] args) throws IOException{
get(3000000);//题目数据范围,N最大值为3*10^6,将2~3*10^6中每一个数的最小质因子全部求出
for(int i=2;i<=3000000;i++) {
ans[i] = ans[i] + ans[i-1];//求前缀和,此时ans[i]中存放的数就是2~i中每一个数的最小质因子的和
}
int n = Integer.parseInt(in.readLine());
while(n-->0) {
out.println(ans[Integer.parseInt(in.readLine())]);
}
out.flush();
}
//找出每个数的质因子
static void get(int n) {
for(int i=2;i<=n;i++) {
if(isprime[i])//i不是质数直接跳过,不考虑,i不能作为筛除条件
continue;
ans[i] = i;//i为素数,素数的最小质因子就是其本身
for(int j=2;j<=n/i;j++) {//j为倍数,将素数i的j倍数标记为合数,并将此数的最小质因子标记为i
if(!isprime[j*i]) {//判断是否已经被标记过
isprime[j*i] = true;//将i*j标记为合数
ans[j*i] = i;//j*i的最小质因子是i
}
}
}
}
}
回文数
判断回文数
思路:将数字转换为字符串类型后,将此字符串倒转后,判断与原字符串是否相同
public static boolean check(int m){
return Integer.toString(m).equals(new StringBuffer(Integer.toString(m)).reverse().toString());
}
判断数组中元素是否相同
思路:若数组中元素全部相同,则数组中的最大值应当==最小值。
public static boolean check(int[] n){
Arrays.sort(n);
return n[0]==n[n.length-1];
}
思路:利用Set集合自动去重,将数组中所有元素全部添加到集合中后,如果集合中只有一个元素,则表示数组中所有元素全部相同。
public static boolean check(int[] n){
Set<Integer> set = new HashSet<>();
for(int i=0;i<n.length;i++) {
set.add(n[i]);
}
return set.size()==1;
}
日期+星期模拟
public static Main{
static int[] date = {0,31,28,31,30,31,30,31,31,30,31,30,31};//存储每月天数
static int y = 2001,m = 1;d = 1,week = 1;//初始年,月,日,星期(根据题意选择是否需要)
//week==0,表示周日,week==1,表示周一 ... week==6,表示周六
public static void main(String[] args){
int ans = 0;//计数
while(y!=9999 || m!=12|| d!=31){//设置日期判断范围
//判断闰年(满足其一即可):
//1.可以整除400
//2.可以整除4但不能整除100
if(y%400==0 || (y%4==0&& y%100!=0) date[2] = 29;
else date[2] = 28;
if(check()) ans++;//满足条件,计数器++;
d++;
week++;
week%=7;
if(d>date[m]){
d = 1;
m++;
}
if(m>12){
m = 1;
y++;
}
}
if(check()) ans++;//之前结束日期并未判断,判断结束日期
System.out.println(ans);
}
public static boolean check(){}//根据题目要求完成
}
约数
唯一分解定理

n的质因数个数----唯一分解定理
public static int num(long n){
int ans = 0;
for(int i=2;i<=n/i;i++){
while(n%i==0){
ans++;
n/=i;
}
}
if(n>1)
ans++;
return ans;
}
n的约数个数----唯一分解定理
public static int num(int n){
int cnt = 1;//乘法初始值为1
int bak = n;//备份n
for(int i=2;i*i<=n;i++){
int sum = 0;
while(bak%i==0){
sum++;
bak = bak / i;
}
cnt = cnt * (sum + 1);
}
if(bak>1) cnt*=2;
return cnt;
}
求n!的约数个数----唯一分解定理
public static long num(int n){
int[] prime = new int[n+1];//prime[i]表示素数i这个因子出现的次数
for(int i=2;i<=n;i++){
int bak = i;
for(int j=2;j*j<=bak;j++){
int sum = 0;
while(bak%j==0){
prime[j]++;
bak = bak / j;
}
}
if(bak>1) prime[bak]++;
}
long ans = 1;
for(int i=2;i<=n;i++){
if(prime[i]>1)
ans = ans * (prime[i]+1);
}
return ans;
}
例题:数数

思路:将这个区间中的每一个数都根据唯一分解定理进行拆分,统计有多少个数的拆分结果为12
import java.util.Scanner;
public class 数数 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int ans = 0;
for(int i=2333333;i<=23333333;i++)
if(num(i)==12)
ans++;
System.out.println(ans);
}
static int num(int n) {
int ans = 0;
for(int i=2;i<=n/i;i++) {
while(n%i==0) {
n/=i;
ans++;
}
}
if(n>1)
ans++;
return ans;
}
}
例题:求阶乘

思路:
1.根据唯一分解定理可知:每一个数都可以写为 n 个素数的乘积;
2.如果一个数的结尾有 0 的存在,那么这个数分解后一定有 2 和 5 (素数中,只有2 * 5才能使结尾产生 0 );
3.从 1 ~ N ,将每一个数都分解后,2 的数量一定比 5 多( 2 每隔两个数就会最少出现一个,5 每隔5个数,最少出现一个),那么,N!末尾 0 的数量,就是将 1 ~ N 中每个数分解后,5 的数量;
4.如果用一个循环从 5 开始,每次 +5 ,判断这些数可以拆分出几个 5 ,然后去找结尾有 k 个 0 的最小的 N 是多少,这个方法结果正确,但是时间复杂度会比较高,所以借助二分,去找到结尾有 k 个 0 的最小的 N 是多少;
5.用二分去查找,就必须做到:已知 N ,求出 1 ~ N 中可以拆分出多少个 5 ,以 125 为例,因为每五个数才拆分出 5 ,所以,如果 1~125 都只拆一个 5 ,则可以拆分出 125 / 5 共 25 个 5 ,拆分后的结果为 1 ~ 25 ,然后继续拆分 5 ,1 ~ 25 可以拆分出 25 / 5 个 5 ,拆分后结果为 1 ~ 5 ,1 ~ 5 可以拆分出 5 / 5 个 5 ,最后剩余 1 ,1 无法继续拆分出 5 ,所以 125 可以拆分出 25 + 5 + 1 = 31 个 5 ;
6.二分:如果mid拆分出的 5 的数量 >= k,那么可以 right = mid ,反之left = mid + 1,二分结果后,还需要判断它是否确实能拆分出 k 个 5 ,因为存在一个 N! 能恰好末尾有 k 个 0 ;
import java.util.Scanner;
public class 求阶乘 {
public static long find(long x) {//求x能拆分出多少个5
long res = 0;
while(x != 0) {
res = res + x / 5;
x/=5;
}
return res;
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
long k = sc.nextLong();
long l = 0,r = 100000;//防止溢出
while(l < r) {
long mid = (l + r) / 2;
if(k <= find(mid)) {
r = mid;
}else {
l = mid + 1;
}
}
if(find(r) != k) {//确保有解
System.out.println(-1);
}else {
System.out.println(r);
}
}
}
第二章 字符串基础
常用API
String m = "abcde";
char ch = m.charAt(String n);//获取字符串m的第(n+1)个字符
int length = m.length();//获取字符串m的长度
boolean flag = m.equals(String n);//判断字符串m和n是否相等,严格区分大小写
boolean flag = m.equalsIgnoreCase(String n);//判断字符串m和n是否相等,不区分大小写
int len = m.index(String s);//返回字符串s在m中第一次出现的位置
int compare = m.compareTo(String anotherString);//按字典序比较两个字符串,若compare>0,m大,若compare<0,m小
String s = m.concat(n);//将字符串n拼接到字符串m的结尾
boolean flag = m.contains(String n);//判断字符串m是否包含字符串n
boolean flag = m.endsWith(String s);//判断字符串m是否以字符串s结尾
String[] s = m.split(" ");//根据正则表达式拆分字符串m
String s = m.trim();//删除字符串m的前导空格和尾部空格
String s = m.subString(int i,int j);//截取字符串m中下标为i至下标为j-1的部分,即[i,j);
...
周期串
思路:从 1 开始枚举周期 T 的大小,然后判断每个周期内的对应字符是否相同,如果不同,则直接判断下一个 T 。
public static int cycle(String s){
char[] ch = s.toCharArray();
int T;
for(T=1;T<=ch.length;T++){
if(ch.length%T==0){//周期串的长度一定是周期T的倍数
boolean flag = true;
for(int start = T;start<ch.length;start++){
if(ch[start]!=ch[start%T]){
flag = false;
break;
}
}
if(flag){
break;
}
}
}
return T;
}
思路:pos 表示第二行的字符串向右移动的格数,如果移动后,第二行的字符串与第一行字符串对应位置的字符全部相同,则 pos 就是这个字符串的周期。

public static int cycle(String s){
String m = s+s;
int pos;
for(pos=1;pos<=s.length();pos++){
if(s.length()%pos!=0)
continue;
String x = m.substring(pos,pos+s.length());
if(x.equals(s))
break;
}
return pos;
}
思路:如果一个字符串 sub 是字符串 s 的周期,那么将字符串 s 中所有的 sub 全部替换为空字符串之后,字符串的长度如果为 0 ,就表示字符串 sub 是字符串 s 的周期。
public static int cycle(String s){
for(int i=1;i<=s.length();i++){
if(s.length()%i==0){
String sub = s.substring(0,i);
if(s.replace(sub,"").length()==0)
return i;
}
}
return 0;
}
例题:重复字符串
题目链接:重复字符串 - 蓝桥云课 (lanqiao.cn)

思路:已知重复次数为 K ,那么周期就是 S.length() / K ,然后只需要求出每一个周期的第 i 个字符,出现次数最多的字符是哪个,然后将其余字符全部改为它,那么就将 S 改为了重复 K 次的字符串,此时修改次数也是最少的。以abdcbbcaabca , 重复 3 次为例:
将此字符串拆分为三个部分后,每个周期写在一行,结果为:
abdc bbca abca
只需要求出每一个竖列出现次数最多的字符出现的次数,然后将其余字符全部改为它,那么这一列修改次数为(K - max),然后将每一列的结果加起来,即为答案。
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
public class 重复字符串 {
static BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
public static void main(String[] args) throws IOException {
int n = Integer.parseInt(in.readLine());
String a = in.readLine();
if(a.length()%n!=0 || n>a.length()) {
System.out.println(-1);
return;
}
int t = a.length() / n;
int index = 0;
char[][] ch = new char[n][t];
for(int i=0;i<n;i++)
for(int j=0;j<t;j++)
ch[i][j] = a.charAt(index++);
int ans = 0;
for(int i=0;i<t;i++) {
int[] num = new int[26];
int max = 0;
for(int j=0;j<n;j++) {
num[ch[j][i]-'a']++;
if(max<num[ch[j][i]-'a']) {
max = num[ch[j][i]-'a'];
}
}
ans = ans + (n-max);
}
System.out.println(ans);
}
}
第三章 排序
冒泡排序
思路:每一次循环将最大值 / 最小值放于向后移动。
public static int[] sort(int[] a){
for(int i=0;i<a.length-1;i++){
for(int j=0;j<a.length-1-i;j++){
if(a[j]>a[j+1]){
int temp = a[j+1];
a[j+1] = a[j];
a[j] = temp;
}
}
}
return a;
}
插入排序
思路:第 i 趟,把第 i 个元素放到前 i - 1 个有序的序列中 。
public static int[] InsertSort(int[] a){
for(int i=1;i<a.length;i++){
int temp = a[i];//处理第i个元素
int j = i-1;
for(;j>=0 && a[j]>temp;j--){
a[j+1] = a[j];//大的元素往后移
}
a[j+1] = temp;
}
return a;
}
选择排序
思路:第 i 趟把从 i ~ 结尾最小的元素找到,放到 i 位置。
public static int[] SelectedSort(int[] a){
for(int i=0;i<a.length;i++){
int min = i;//存放i+1到最后最小的元素所在的下标
for(int j=i+1;j<a.length;j++){
if(a[j]<a[min])
min = j;
}
int temp = a[i];
a[i] = a[min];
a[min] = temp;
}
return a;
}
希尔排序
思路:将排序的区间分成若干个有跨度的子区间,对每一个子区间,进行插入排序,跨度不断 / 2 ,最终当跨度为 1 的时候,进行一个插入排序。
public static int[] shell(int[] a){
for(int gap = a.length/2;gap>0;gap/=2){
//对每一分组进行直接插入排序
for(int i=gap;i<a.length;i++){
int j = i;
while(j-gap>=0 && a[j-gap]>a[j]){//大的往后移动
int temp = a[j];
a[j] = a[j-gap];
a[j-gap] = temp;
j = j-gap;//下一次继续从分组的前一个位置开始
}
}
}
return a;
}
计数排序
思路:找出数组中的最大值和最小值,每个数都是在 min 和 max 之间,用一个长度为(max - min + 1)的数组 c 来存储每一个数出现的次数,然后将数组 c 转换为前缀和数组,则 c[ i ],就表示不大于(i+min)的元素的个数,按照 c 数组还原排序结果。
public static void countSort(int[] a){
int[] b = new int[a.length];
int max = a[0];min = a[0];
for(int i=0;i<a.length;i++){
if(a[i]>max) max = a[i];
if(a[i]<min) min = a[i];
}
int dis = max - min + ;
int[] c = new int[dis];
for(int i=0;i<a.length;i++)
c[a[i]-min]++;
for(int i=1;i<c.length;i++)
c[i] = c[i] + c[i-1];
for(int i=a.length-1;i>=0;i--){
b[c[a[i]-min]-1] = a[i];
c[a[i]-min]--;
}
System.out.println(Arrays.toString(b));
}
第四章 数据结构基础
链表
为什么要用链表
数组作为一个顺序储存方式的数据结构,可是有大作为的,它的灵活使用为我们的程序设计带来了大量的便利;但是,数组最大的缺点就是我们的插入和删除时需要移动大量的元素,所以呢,大量的消耗时间,以及冗余度难以接收。
链表可以灵活地去解决这个问题,插入删除操作只需要修改指向的对象就可以了,不需要进行大量的数据移动操作。
单链表
初始化
static class Node{//定义结点类
int value;//本身的值
Node next;//指向下一个结点
public Node(int value, Node next) {
this.value = value;
this.next = next;
}
}
Node head = new Node(-1,null);//头结点
Node end = new Node(-1, null);//尾结点
Node per = head;
for(int i=1;i<=10;i++) {
per.next = new Node(i, null);
per = per.next;
}
per.next = end;
插入
插入前:
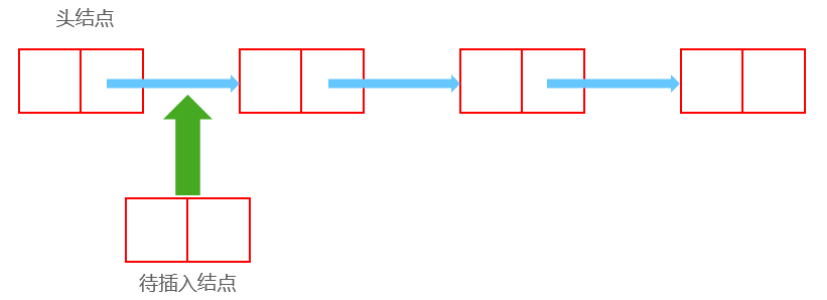
插入后:
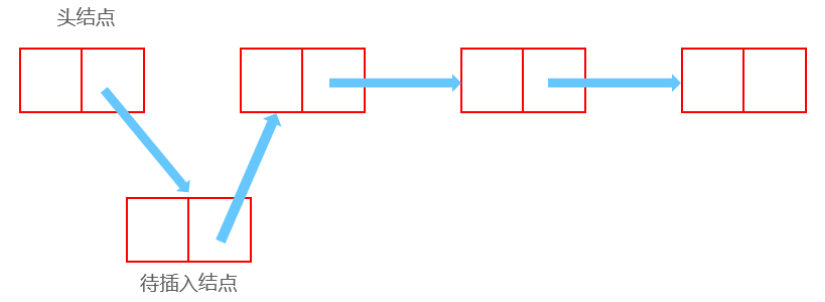
Node now;//待插入结点
now.next = head.next;//此节点的next为插入位置上一个结点的下一个结点
head.next = now;//此节点位置的上一个结点的下一个结点为now
删除
删除前:
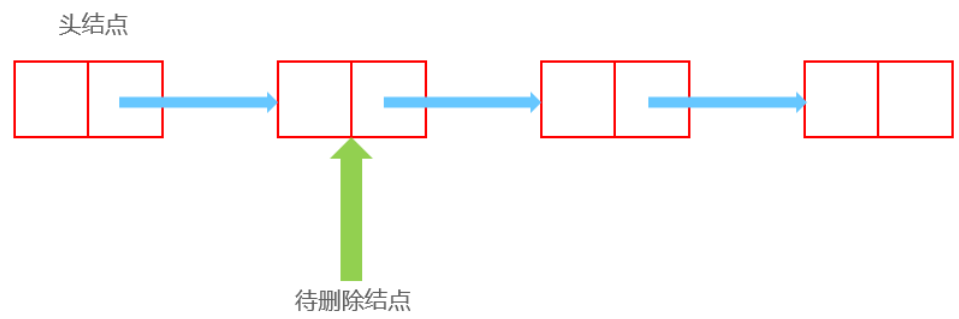
删除后:
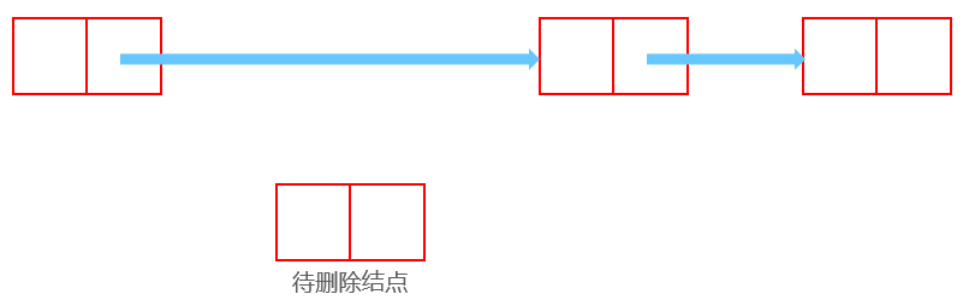
Node now;//待删除结点
head.next = now.next;
双链表
初始化
static class N{
N last;
int value;
N next;
public N(N last, int value, N next) {
this.last = last;
this.value = value;
this.next = next;
}
}
Node first = new Node(null,-1,null);//头结点
Node end = new Node(null,-1, null);//尾节点
Node per = first;
for(int i=1;i<=10;i++) {
per.next = new N(per,i, null);
per = per.next;
}
end.last = per;
per.next = end;
插入
插入前:
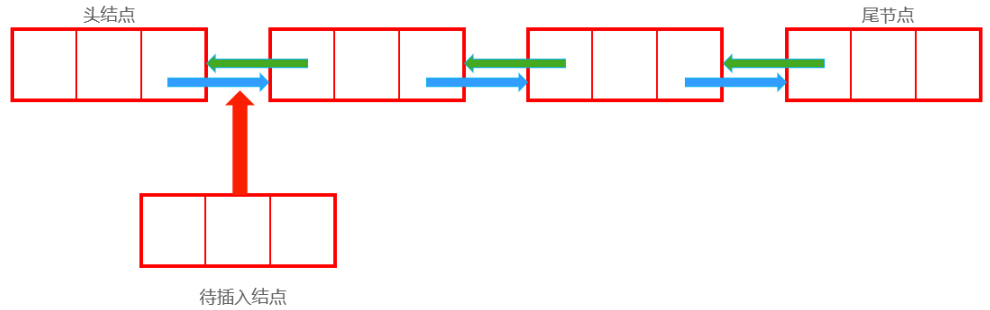
插入后:
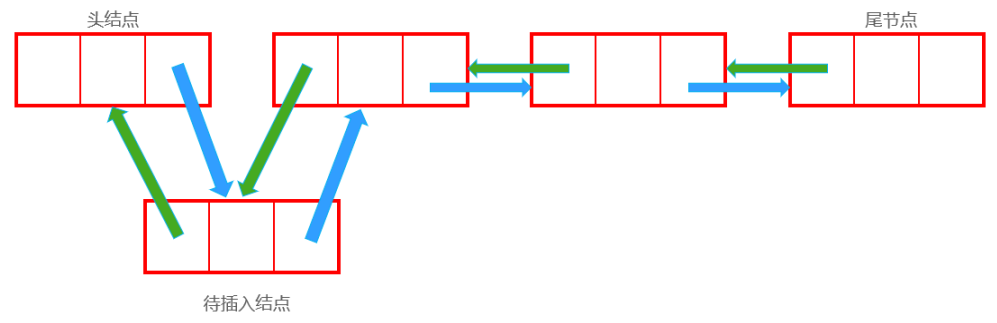
Node now;//待插入结点
now.next = first.next;
first.next.last = now;
first.next = now;
now.last = first;
删除
删除前:
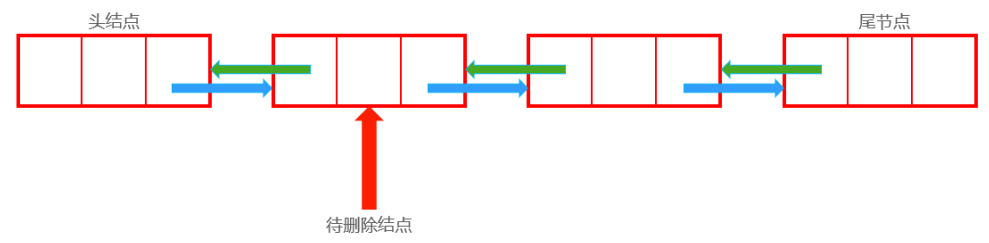
删除后:
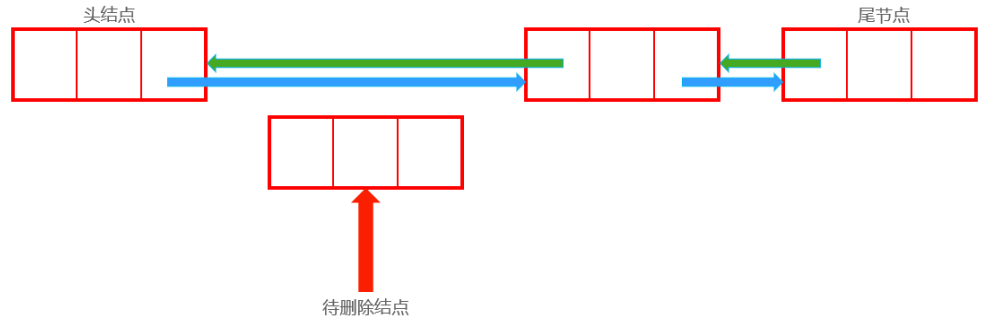
Node now;//待删除结点
now.last.next = now.next;
now.next.last = now.last;
例题:左移右移(双链表解法)

思路:
1.创建双链表并完成初始化,初始元素为 1 ~ n;
2.无论 x 左移或右移,都要先将 x 从原位置删除,为了便于获取 x 对应的 Node 结点,用 Map 存储 x 和 value 为 x 的结点;
3.如果 x 为左移,就将 x 对应的 Node 结点插入到头结点后;
4.如果 x 为右移,就将 x 对应的 Node 结点插入到尾节点前;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.util.HashMap;
import java.util.Map;
public class 左移右移_双链表 {
static class Node{
Node up;
int value;
Node down;
public Node(Node up, int value, Node down) {
this.up = up;
this.value = value;
this.down = down;
}
}
public static void main(String[] args) throws IOException{
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
String[] s = in.readLine().split(" ");
int n = Integer.parseInt(s[0]);
int m = Integer.parseInt(s[1]);
Map<Integer, Node> map = new HashMap<>();
Node first = new Node(null, -1, null);
Node last = new Node(null, -1, null);
Node no = first;
for(int i=1;i<=n;i++) {
no.down = new Node(no, i, null);
no = no.down;
map.put(i, no);
}
last.up = no;
no.down = last;
for(int i=0;i<m;i++) {
s = in.readLine().split(" ");
char ch = s[0].charAt(0);
int x = Integer.parseInt(s[1]);
Node node = map.get(x);
node.up.down = node.down;
node.down.up = node.up;
if(ch=='L') {
node.down = first.down;
first.down.up = node;
first.down = node;
node.up = first;
}else {
node.up = last.up;
last.up.down = node;
node.down = last;
last.up = node;
}
}
no = first.down;
while(no!=last) {
System.out.print(no.value+" ");
no = no.down;
}
}
}
栈
栈
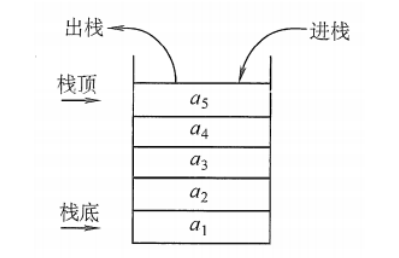
栈(Stack):是只允许在一端进行插入或删除的线性表。首先栈是一种线性表,但限定这种线性表只能在某一端进行插入和删除操作。
栈顶(Top):线性表允许进行插入删除的那一端。
栈底(Bottom):固定的,不允许进行插入和删除的另一端。
常用方法
Stack<Integer> stack = new Stack();
boolean is = stack.isEmpty();//判断此栈是否为空
int n = stack.peek();//获取栈顶的元素,但不删除
int m = stacl.pop();//获取并删除栈顶的元素
stack.push(10);//将10压入栈中
stack.clear();//清空栈
判断括号序列是否合法
public static boolean check(String s){
Stack<Character> stack = new Stack();
char[] ch = s.toCharArray();
for(int i=0;i<ch.length;i++){
if(ch[i]=='(')
stack.push(ch[i]);
else if(stack.isEmpty())
return false;
else
stack.pop();
}
return stack.isEmpty();
}
队列
队列
队列(queue)是一种先进先出的、操作受限的线性表。
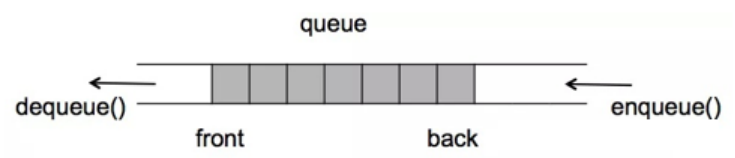
队列这种数据结构非常容易理解,就像我们平时去超市买东西,在收银台结账的时候需要排队,先去排队的就先结账出去,排在后面的就后结账,有其他人再要过来结账,必须排在队尾不能在队中间插队。
常用方法
Queue<Integer> queue = new LinkedList<>();
queue.peek();//获取队头元素,但不删除
queue.poll();//获取并删除队头元素
queue.clear();//清空队列
queue.push(11);//将11存放到队列中
例题:左移右移(栈 + 队列解法)

思路:
1.如果一个数先移动到最左边,再移动到最右边,那么最后输出的时候这个数一定是在最右边,也就是一个数最终出现在哪里,以他最后一次出现为准;
2.为了避免一个数重复判断,而且要以他最后一次出现时的 L 和 R 操作为最终操作,所以可以先将全部输入分别存放到 char 类型数组和 int 类型数组中,然后逆序判断,并且用一个数组来表示这个 x 有没有出现过;
3.因为要对输入做逆序操作,所以,逆序时最后出现的 L 对应的 x 在输出的最前面,然后之后出现的 L 对应的 x 依次输出,即先入先出,可以用队列来存储进行 L 操作的 x ;
4.逆序时最后出现的 R 对应的 x 在输出的最后面,然后之后出现的 R 对应的 x 依次在前,即后入先出,可以用栈来存储进行 R 操作的 x ;
5.输出时,先输出队列中的元素,然后将 1 ~ n 中没有出现过的值按序输出,最后输出栈中的元素;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;
public class 左移右移_栈_队列 {
public static void main(String[] args) throws IOException{
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
String[] s = in.readLine().split(" ");
int n = Integer.parseInt(s[0]);
int m = Integer.parseInt(s[1]);
int[] a = new int[n+1];
char[] c = new char[m];
int[] x = new int[m];
for(int i=0;i<m;i++) {
s = in.readLine().split(" ");
c[i] = s[0].charAt(0);
x[i] = Integer.parseInt(s[1]);
}
Stack<Integer> r = new Stack<>();
Queue<Integer> l = new LinkedList<>();
for(int i=m-1;i>=0;i--) {
if(a[x[i]]==0) {//判断x[i]是否出现过
a[x[i]] = 1;//若x[i]没有出现过
if(c[i]=='L')
l.add(x[i]);
else
r.push(x[i]);
}
}
while(l.size()!=0) //输出队列中元素
System.out.print(l.poll()+" ");
for(int i=1;i<=n;i++)
if(a[i]==0) //a[i]为0,表示i没有出现过
System.out.print(i+" ");
while(r.size()!=0) //输出栈中元素
System.out.print(r.pop()+" ");
}
}
第五章 分治算法
归并排序
思路:先把数组从中间分成前后两部分,然后分别对前后两部分进行排序,再将排好序的两部分数据合并在一起
public static void mergeSort(int[] a,int left,int right){//待排序数组,要排序的范围[left,right]
int mid = (left+right)>>1;
if(left<right){
mergeSort(a,left,mid);
mergeSort(a,mid+1,right);
merge(a,left,mid,right);
}
}
public static void merge(int[] a,int left,int mid,int right){
int[] temp = new int[right-left+1];//临时数组,用来归并
int i=left,j=mid+1,k=0;//左半段用i指向,右半段用j指向,temp数组用k指向
while(i<=mid && j<=right){
if(a[i]<a[j])
temp[k++] = a[i++];
else
temp[k++] = a[j++];
}
while(i<=mid) temp[k++] = a[i++];
while(j<=right) temp[k++] = a[j++];
for(int x=0;x<temp.length;x++){
a[left+x] = temp[x];
}
}
快速排序
思路:
(1)首先设定一个分界值,通过该分界值将数组分成左右两部分。
(2)将大于或等于分界值的数据集中到数组右边,小于分界值的数据集中到数组的左边。此时,左边部分中各元素都小于分界值,而右边部分中各元素都大于或等于分界值。
(3)然后,左边和右边的数据可以独立排序。对于左侧的数组数据,又可以取一个分界值,将该部分数据分成左右两部分,同样在左边放置较小值,右边放置较大值。右侧的数组数据也可以做类似处理。
(4)重复上述过程,可以看出,这是一个递归定义。通过递归将左侧部分排好序后,再递归排好右侧部分的顺序。当左、右两个部分各数据排序完成后,整个数组的排序也就完成了。
public static void quickSort(int[] a,int left,int right){
if(left>right) return;//区间擦肩而过,无效,不需要进行递归
int i=left,j=right,temp = a[left];//a[left]作为基准点
while(i!=j){
while(a[j]>=a[temp] && j>i)
j--;//只要a[j]大于基准点继续往前移动j
if(j>i)
a[i++] = a[j];
while(a[i]<=a[temp] && i<j)
i++;
if(i<j)
a[j--] = a[i];
}
a[i] = temp;//基准点元素放到最终位置
quickSort(a,left,i-1);
quickSort(a,i+1,right);
}
快速幂
思路:每一步都把指数分成两半,而相应的底数做平方运算。这样不仅能把非常大的指数给不断变小,所需要执行的循环次数也变小,而最后表示的结果却一直不会变。
例:3^10^ = 3*3*3*3*3*3*3*3*3*3 ,尽量想办法把指数变小来,这里的指数为10。
3^10^=(3*3)(3*3)(3*3)(3*3)(3*3)
3^10^=(3*3)^5^
3^10^=9^5^
此时指数由10缩减一半变成了5,而底数变成了原来的平方,求3^10^原本需要执行10次循环操作,求9^5^却只需要执行5次循环操作,但是3^10^却等于9^5^,用一次(底数做平方操作)的操作减少了原本一半的循环量,特别是在幂特别大的时候效果非常好,例如2^10000^=4^5000^,底数只是做了一个小小的平方操作,而指数就从10000变成了5000,减少了5000次的循环操作。
现在问题是如何把指数5变成原来的一半,5是一个奇数,5的一半是2.5,但是指数不能为小数,因此不能简单粗暴地直接执行5/2,然而,这里还有另一种方法能表示9^5^,9^5^=9^4^*9^1^
此时抽出了一个底数的一次方,这里即为9^1^,这个9^1^先单独移出来,剩下的9^4^又能够在执行“缩指数”操作了,把指数缩小一半,底数执行平方操作。9^5^=81^2^*9^1^
把指数缩小一半,底数执行平方操作,9^5^=6561^1^*9^1^
此时,发现指数又变成了一个奇数1,按照上面对指数为奇数的操作方法,应该抽出了一个底数的一次方,这里即为6561^1^,这个6561^1^先单独移出来,但是此时指数却变成了0,也就意味着我们无法再进行“缩指数”操作了。
9^5^=(6561^0^)(9^1^)(6561^1^)=1(9^1^)(6561^1^)=(9^1^)(6561^1^)=9*6561=59049
能够发现,最后的结果是9*6561。所以能发现一个规律:最后求出的幂结果实际上就是在变化过程中所有当指数为奇数时底数的乘积。
继续优化:
b%2==1可以用更快的“位运算”来代替,例如:b&1。因为如果b为偶数,则其二进制表示的最后一位一定是0;如果b是奇数,则其二进制表示的最后一位一定是1。将他们分别与1的二进制做“与”运算,得到的就是b二进制最后一位的数字了,是0则为偶数,是1则为奇数。例如9是奇数,则9&1=1;而8是偶数,则8&1=0;因此奇偶数的判断就可以用“位运算”来替换了。
m = m / 2也可以用更快的移位操作来代替,例如:6的四位二进制为0110,而6/2=3,3的四位二进制为0011,可以发现,a的一半,结果为a的二进制码向右移一位,即m >>=1。
public static long num(long n, long m, long p) {
long result = 1;
while (m > 0) {
if ((m & 1 ) == 1) {
result = result * n % p;
}
m >>= 1;
n = (n * n) % p;
}
return result;
}
第六章 搜索
全排列
DFS解法
思路:将此过程看做一棵树,每一个结点下都会有 n 个结点表示下一个数,首先先将全部 n^n^ 个结果全部得出,然后剪枝,减去有重复数字出现的情况。
public static void dfs(int depth,String ans,int n){//当前深搜的层数,目前的结果,目标层数
if(depth==n){//当前深搜层数=目标层数
System.out.println(ans);
return;
}
for(int i=1;i<=n;i++){
if(!ans.contains(i+""))//只有当还没有用过i的时候,才会在现在的基础上继续往下拓展
dfs(depth+1,ans+i;n);//进入下一层,ans记录为进入下一层的值,n不变
}
}
BFS解法
思路:先将有重复数字的结果得出,每一个数后都可以跟 n 中可能,那么将这 n 中可能存入队列中,然后重复此过程,直到字符串的长度为 n 时,得到结果;剪枝,如果这个数字已经用过了,就直接只用下一个数字。
public static void bfs(int n){
Queue<String> queue = new LinkedList<>();
for(int i=1;i<=n;i++)
queue.offer(i+"");
while(!queue.isEmpty()){
String now = queue.poll();
for(int i=1;i<=n;i++){//每个结点都向下产生n个结果
if(now.contains(i+""))//i已经使用过了
continue;
String son = head + i;
if(son.length()==n)
System.out.println(son);
else
queue.offer(son);
}
}
}
整数划分
思路:对 n 进行划分后, n 可以被不超过 n 个数累加得到,进行累加的每一个数,也可以被不超过它本身个数累加得到。
public static void dfs(int n,int nowget,int max,String ans){//要划分的数,现在已经得到的值,目前划分已经用到的最大值,具体拆分方法
if(nowget==n){
ans = ans.substring(0,ans.length()-1);
System.out.println(n+"="+ans);
return;
}
for(int i=1;i<=n-nowget;i++){//从nowget累加到n
if(i>=max)//只有当下一个数不小于我之前用过的最大值时,才能保证整个结果为非递减
dfs(n,nowget+i,i,ans+i+"+");
}
}
例题
例题:路径之谜
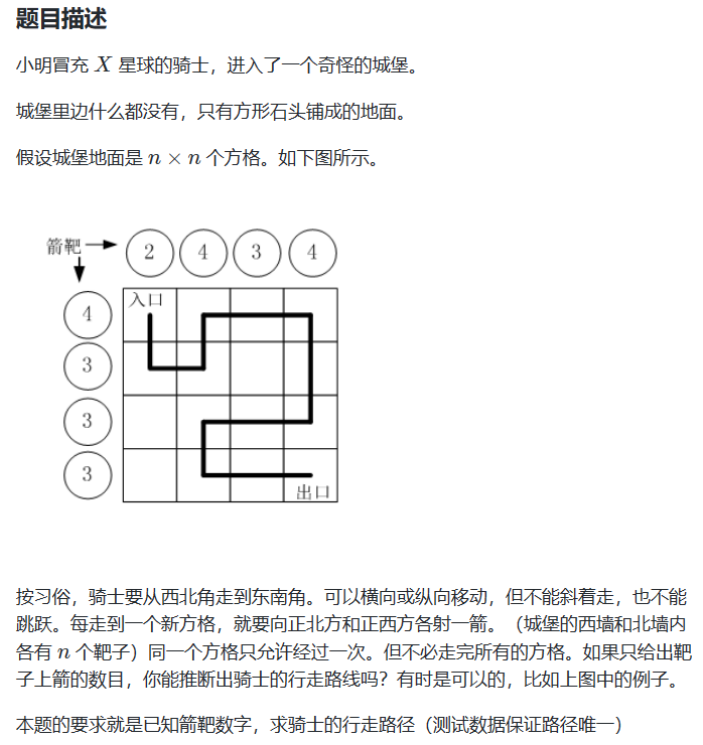
思路:
1.从入口点开始,到达每一个点都将对应位置北墙和西墙的箭靶数减一,每一个点,都可以继续向四个方向继续前进(前提是这个点没有走过,在城堡范围内,且这个点对应的两个箭靶的数字不为 0 )。
2.如果已经到了终点,就要判断现在每一个箭靶上的数字是否都已经变为 0 ,如果是,那么此时走的路径就是正确解,否则就需要回溯,考虑其他的行走路线。
3.回溯:因为要从已经走过的点退回来,所以在已经走过的点上射的箭要收回,箭靶数加一,并且标记此点为还没有走过。
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
public class 路径之谜 {
static int[] path;//记录最终路径,因为底面为n*n,所以走出需要2*n步
static int n;
static int[] cntx;//存储北墙箭靶数字
static int[] cnty;//存储西墙箭靶数字
static boolean[][] visited;//判断此点有没有走过
static int dx[] = {1, 0, -1, 0};//到下一个点x坐标的变化量
static int dy[] = {0, 1, 0, -1};//到下一个点y坐标的变化量
static BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
public static void main(String[] args) throws IOException {
n = Integer.parseInt(in.readLine());
cntx = new int[n];
cnty = new int[n];
path = new int[n * n];
visited = new boolean[n][n];
String[] s = in.readLine().split(" ");
for (int i = 0; i < n; i++) {
cntx[i] = Integer.parseInt(s[i]);
}
s = in.readLine().split(" ");
for (int i = 0; i < n; i++) {
cnty[i] = Integer.parseInt(s[i]);
}
dfs(0, 0, 0);//从0,0位置开始走,目前走了0步
}
private static void dfs(int x, int y, int step) {
path[step] = y * n + x; //将该点编号记录到路径中
visited[x][y] = true;//将该点标记为已经走过的状态
cntx[x]--;//拔掉对应北墙的箭
cnty[y]--;//拔掉对应西墙的箭
if (x == n - 1 && y == n - 1 && check()){//判断是否到达终点
for (int i = 0; i <= step; i++){//输出答案
System.out.print(path[i]+" ");
}
return;
}
for (int i = 0; i < 4; i++){//上下左右四个方向搜索下一步
int xx = x + dx[i], yy = y + dy[i];
//下一步(xx,yy)未走过且在地图范围内
if (0 <= xx && xx <= n-1 && yy >= 0 && yy <= n-1&& !visited[xx][yy] ){
if (cntx[xx] > 0 && cnty[yy] > 0){//该点对应箭靶上有箭,说明该点可以走
dfs(xx, yy, step + 1);//搜索下一步
//要从xx,yy点回来,在xx,yy点射的箭要复原,并重新标记xx,yy点没有走过
visited[xx][yy] = false;
cntx[xx]++;
cnty[yy]++;
}
}
}
}
private static boolean check() {//判断到达终点时,是否箭靶数都已经归零
for (int i = 0; i < n; i++) {
if (cntx[i] != 0 || cnty[i] != 0)
return false;
}
return true;
}
}
例题:迷宫

思路:从起点开始,将从此点能到达的点存储到队列中,每次获取并删除队列中的第一个元素,并将其能到达且还未到达过的点(若此点已经到达过,则表示当前处理的这条路径不是最短路径)存储到队列中,若已经到达终点,则此路径为最短路径。如果队列中已经没有元素,但仍未到达迷宫终点,则表示此迷宫无解
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.util.LinkedList;
import java.util.Queue;
public class 迷宫 {
static int num;//存储迷宫最短路径所需要的步数
static int xsize = 30;//迷宫大小30行50列
static int ysize = 50;
static char[][] arr = new char[xsize][ysize];//存储迷宫:0表示路,1表示墙
static boolean[][] help = new boolean[xsize][ysize];//判断此点是否已经做过
static int[][] dir = {{1,0},{0,-1},{0,1},{-1,0}};//四个方向横纵坐标的变化量
static char[] sign = {'D','L','R','U'};//表示四个方向
public static void main(String[] args) throws IOException {
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
for(int i=0;i<xsize;i++){
arr[i] = in.readLine().toCharArray();
}
out.println(bfs());
out.print(num);//额外输出最短路径需要多少步
out.flush();
}
private static String bfs() {
Queue<Node> list = new LinkedList<>();//队列
int x = 0;
int y = 0;
int runnum = 0;
list.add(new Node(x,y,"",runnum));//将起点存储到队列中
while(!list.isEmpty()){//判断队列是否为空,若为空,则此迷宫没有通路
Node now = list.poll();//获取队列中的第一个元素并删除
help[now.x][now.y] = true;//将此点标记为已经走过
for(int i=0;i<4;i++){//循环四次,对四个方向进行处理
int xx = now.x + dir[i][0];//移动后的x坐标
int yy = now.y + dir[i][1];//移动后的y坐标
//此点在迷宫范围内,未走过,不是墙
if(check(xx,yy) && help[xx][yy]==false && arr[xx][yy]=='0'){
list.add(new Node(xx,yy,now.num + sign[i],now.runnum + 1));//将此点存入队列中
if(xx==xsize-1 && yy==ysize-1){//如果已经到了迷宫终点
num = now.runnum + 1;//所需步数+1(now.runnum是到达迷宫终点前一步所需要的步数)
return now.num + sign[i];//返回通过迷宫的方式
}
}
}
}
return "";//空字符串,表示此迷宫无通路
}
private static boolean check(int xx, int yy) {//判断此点是否在迷宫范围内
return xx>=0 && yy>=0 && xx<xsize && yy<ysize;
}
static class Node{
int x;//x坐标
int y;//y坐标
int runnum;//到达此点最短步数
String num;//到达此点的方式
public Node(int x, int y,String num ,int runnum) {
super();
this.x = x;
this.y = y;
this.num = num;
this.runnum = runnum;
}
}
}
第七章 贪心
基本概念
所谓贪心算法是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,它所做出的仅仅是在某种意义上的局部最优解。 贪心算法没有固定的算法框架,算法设计的关键是贪心策略的选择。必须注意的是,贪心算法不是对所有问题都能得到整体最优解,选择的贪心策略必须具备无后效性(即某个状态以后的过程不会影响以前的状态,只与当前状态有关。
例题
例题:合并果子

思路:
1.要保证最终耗费的体力最小,那么就可以每次合并都把目前数量最少的两堆果子合并,耗费的体力就是这两堆果子树木的和,然后合并后又可以作为新的一堆果子继续去判断,直到最终只剩一堆。
2.可以借助PriorityQueue优先队列,队列中第一个元素就是最小值,即可每次获取队列中前两个元素,然后将他们的和再次添加至队列中,直到最终队列中只剩一个元素。
3.以题目样例为例:对于数组{pi}={1, 2, 9},Huffman树的构造过程如下:
3.1找到{1, 2, 9}中最小的两个数,分别是 1 和 2 ,
3.2从{pi}中删除它们并将和 3 加入,得到{3, 9},体力消耗为 3 。
3.3找到{3, 9}中最小的两个数,分别是 3 和 9 ,
3.4从{pi}中删除它们并将和 12 加入,得到{12},费用为 12 。
3.5现在,数组中只剩下一个数12,构造过程结束,总费用为3 + 12 = 15。
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.util.PriorityQueue;
import java.util.Scanner;
import java.util.Spliterator;
public class Main {
public static void main(String[] args) throws IOException{
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
int n = Integer.parseInt(in.readLine());
long sum = 0;
PriorityQueue<Long> queue = new PriorityQueue<>();
String[] s = in.readLine().split(" ");
for(int i=0;i<s.length;i++) {
queue.add(Long.parseLong(s[i]));
}
long number = 0;
while(queue.size()!=1) {
long a = queue.poll();//获取最小的一堆
long b = queue.poll();//获取最小的一堆
number = number + ( a + b );//合并这两堆耗费的体力
queue.add((a+b));//将合并后的结果放回优先队列中
}
System.out.println(number);
}
}
第八章 树
树的相关概念
什么是树
树(Tree)是 n ( n ≧ 0 )个结点的有限集。n=0时称为空树。在任意一颗非空树中:有且仅有一个特定的称为根的结点。当n>1时,其余结点可分为 m ( m > 0 ) 个互不相交的有限集T1、T2、T3……、Tm,其中每个集合本身又是一棵树,并且称为根的子树。
树的基本概念
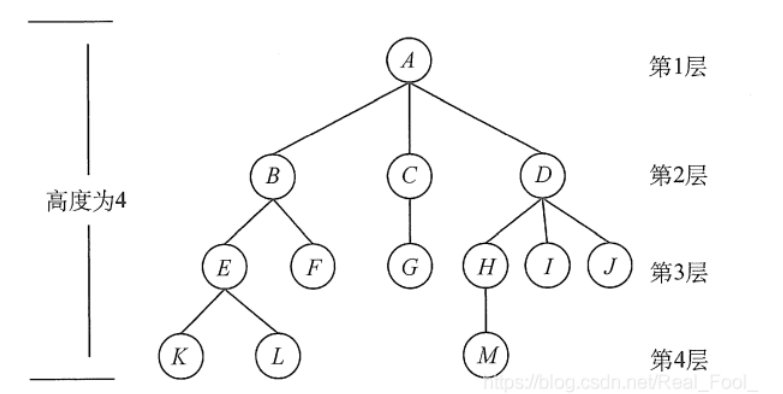
二叉树
什么是二叉树
二叉树是n(n>=0)个结点的有限集合,该集合或者为空集(空二叉树)、或者由一个根结点和两颗互不相交的、分别称为根结点的左子树和右子树的二叉树组成。
二叉树的特点
1.二叉树中每个结点最多有两颗子树,度没有超过2的。
2.左子树和右子树是有顺序的,不能颠倒。
满二叉树
在二叉树中,所有的分支节点都有左子树和右子树,并且所有的叶子都在同一层。
完全二叉树
1.叶子结点只能出现在最下面两层。
2.最下层的叶子一定集中在左部连续位置。
3.倒数第二层,若有叶子结点,一定在右部连续位置。
4.如果结点度为1,则该结点只有左孩子。
5.同样结点的二叉树,完全二叉树的深度最小。
二叉树的创建和嵌套打印
//结点类
public class TreeNode{
int data;//结点存放的数据
TreeNode left;//左孩子
TreeNode right;//右孩子
public TreeNode(int data,TreeNode left,TreeNOde right){
this.data = data;
this.left = left;
this.right = right;
}
}
import java.util.Scanner;
public class Tree{
TreeNode root;//整棵树的根节点
Scanner sc = new Scanner(System.in);
public Tree(){
root = null;
}
public TreeNode createBinaryTree(){//树的创建
TreeNode t;//当前树的根节点
int x = sc.nextInt();
if(x==0) t=null;
else{
t = new TreeNode();
t.data = x;
t.left = createBinaryTree();
t.right = createBinaryTree();
}
return t;
}
public void printTree(TreeNode t){//树的打印
if(t!=null){
System.out.print(t.data);
if(t.left!=null || t.right!=null){
System.out.print("(");
printTree(t.left);
if(t.right!=null) System.out.print(",");
printTree(t.left);
System.out.print(")");
}
}
}
}
前中后序层次遍历
前序遍历
思路:对于每个结点,优先处理结点本身,再处理它的左孩子,最后处理它的右孩子。
public void preOrder(TreeNode root){
if(root!=null){
System.out.print(root.data+" ");
preOrder(root.left);
preOrder(root.right);
}
}
中序遍历
思路:对于每个结点,优先处理它的左孩子,再处理它本身,最后处理它的右孩子。
public void midOrder(TreeNode root){
if(root!=null){
midOrder(root.left);
System.out.print(root.data+" ");
midOrder(root.right);
}
}
后序遍历
思路:对于每个结点,优先处理它的左节点,再处理它的右节点,最后处理它本身。
public void postOrder(TreeNode root){
if(root!=null){
postOrder(root.left);
postOrder(root.right);
System.out.print(root.data+" ");
}
}
层次遍历
思路:广度优先搜索;处理根节点的每一个子结点,再处理子结点的每一个子结点......直至结束。
public void levelOrder(TreeNode t){
Queue<TreeNode> queue = new LinkedList<>();
if(t==null) return;
queue.offer(t);
while(!queue.isEmpty()){
TreeNode head = queue.poll();
System.out.print(head.data);
if(head.left!=null)
queue.offer(head.left);
if(head.right!=null)
queue.offer(head.right);
}
}
求二叉树深度
public int treeDepth(TreeNode root){
if(root==null) return 0;//此结点不存在
return Math.max(treeDepth(root.left),treeDepth(root.right))+1;
}
求二叉树叶子结点个数
public int TreeLeaf(TreeNode root){
if(root==null) return 0;
if(root.left==null && root.right==null) return 1;//此结点没有孩子,表示此结点为叶子结点
else return treeLeaf(root.left) + treeLeaf(root.right);
}
重建二叉树
思路:
1.前序遍历为:根,{左子树},{右子树};可得,前序遍历的第一个结点为根结点;
2.中序遍历为:{左子树},根,{右子树};可得,结点的左侧为它的左孩子树,右侧为它的右孩子树;
3.重复此过程,重建此二叉树;
public static String f(String pre,String mid){//前序遍历结果,中序遍历结果
if(pre.length()==0) return "";
else if(pre.length==1) return pre;
else{
int pos = mid.indexOf(pre.charAt(0));
String left = f(pre.substring(1,pos+1),mid.substring(0,pos));
String right = f(pre.substring(pos+1),mid.substring(pos+1));
return left+right+pre.charAt(0);
}
}
第九章 图
第十章 动态规划
LCS 最长公共子序列
思路:
1.用一个数组 dp[ i ][ j ] 表示 S 字符串中前 i 个字符与 T 字符串中前 j 个字符的最长上升子序列,那么 dp[ i+1 ][ j+1 ] 就是S 字符串中前 i+1 个字符与 T 字符串中前 j+1 个字符的最长上升子序列;
2.如果此时 S 中的第 i+1 个字符与 T 中的第 j+1 个字符相同,那么 dp[ i+1 ][ j+1 ] = dp[ i ][ j ] + 1;
3.如果此时 S 中的第 i+1 个字符与 T 中的第 j+1 个字符不同,那么 dp[ i+1 ][ j+1 ] = Math.max ( dp[ i+1 ][ j ] , dp[ i ][ j+1 ] );
public static int LCS(String s,String t){
int[][] dp=new int[s.length()+1][t.length()+1];
for(int i=1;i<=s.length();i++){
for(int j=1;j<=t.length();j++){
if(s.charAt(i-1)==t.charAt(j-1))
dp[i][j]=dp[i-1][j-1]+1;
else
dp[i][j]=Math.max(dp[i][j-1],dp[i-1][j]);
}
}
return dp[len1][len2];
}